 P o w r ó t
P o w r ó t
| AB Homepage |
 P o w r ó t P o w r ó t
|
Podstawa
Folley i in.; Richardson
Model barw RGB (Red, Green, Blue) jest najczęściej stosowanym standardem przestrzeni barw. Jest to przestrzeń zwarta i taka, że punkt (rgb)=(000) odpowiada w niej czerni, a punkt (111) bieli. Na przekątnej (000)-(111) sześcianu RGB leżą odcienie szarości. Innym wierzchołkom sześcianu odpowiadaja barwy podstawowe: czerwona (010), zielona (100) oraz niebieska (001). Pozostałe barwy wierzchołkowe to żółta (110) oraz magenta (011). Pośrednie wartości natężeń rgb dają w wyniku mieszankę barw, a więc barwę złożoną.
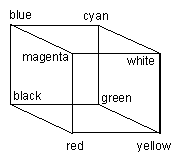
Standard RGB stosowany jest w urządzeniach wyświetlających takich, jak monitory oraz lampy kineskopowe TV. Obok modelu RGB stosuje się często model barw HSB (Hue, Saturation, Brightnes). Inne standardy, takie jak CMYK (Cyan, Magenta, Yellow) stosowane są w drukarstwie .
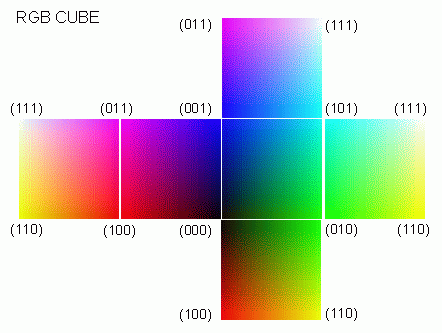
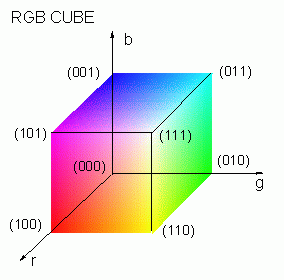
Dalej pokażemy, jak odwzorować w przestrzeń RGB funkcję określoną na zespolonej płaszczyźnie C (lub R2) tak by można było śledzić jej wartości oraz fazy. Metoda ta nadaje się np. do przedstawienia rozpraszania kwantowej paczki falowej na dwuwymiarowym potencjale (patrz Richardson).
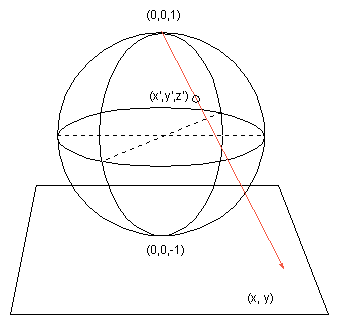
Opisane odwzorowanie jest postaci (patrz również rysunek)
| (1) |
Następny krok polega na zanurzeniu sfery jednostkowej w przestrzeń kolorów. W tym celu zmniejszymy promień sfery do 1/2 i umieścimy jej środek w punkcie (r,g,b) = (1/2, 1/2, 1/2). Oś południe-północ sfery utożsamimy z kierunkiem przekątnej sześcianu RGB (000)-(111), a więc z szarym kierunkiem czerń-biel w przestrzeni barw. W ten sposób biegun południowy, bliski punktowi (0,0,0) w RGB, jest prawie czerny - brak amplitudy, a biegun północny prawie biały - maksymalna amplituda. Aby określić jednoznacznie orientację azymutalną zażądamy by kierunek osi y przebiegał przez maksimum natężenia czerwieni, a więc przez punkt (010) w przestrzeni RGB.
Opisane odwzorowanie dobrze oddaje sytuację dla punktów z sąsiedztwa okręgu jednostkowego. Początek układu oraz punkty w nieskończoności nie są dostatecznie różne. Aby poprawić sytuację, można zamienić sferę parą stożków o wierzchołkach w punktach (0,0,0) i (1,1,1), sklejonych na równiku sfery. W ten sposób nie zepsujemy za bardzo obszaru równikowego i jednocześnie "dodamy więcej punktów" w obszarze biegunów sfery, a więc łatwiej będzie rozróżnić punkty w okolicy początku układu i w nieskończoności (rysunek).
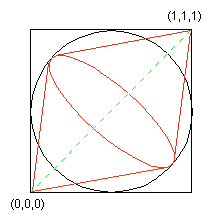
Odwzorowanie to ma postać
| (2) |
Dzieląc przez 2 i obracając tak by osie stożków pokryły się z kierunkiem diagonali sześcianu kolorów oraz przesuwając do środka sześcianu kolorów otrzymamy ostatecznie
| (3) |
| (4) |
| (5) |
Przykład tego typu odwzorowania pokazuje rysunek. Przedstawiona funkcja f(x,y) została tylko pomalowana, tzn. (x,y) ® (r,g,b) z użyciem algorytmu Richardsona bez specjalnych powodów.

Program w JavaTM , który wyznacza kolory podany jest poniżej.
\import java.awt.Color;
...
private Color toRGB(float x, float y){
/ transform (x,y,z) position to color space rgb
float xy, sq, iq, eta, q1, q2, q3, r, g, b;
final float half = 0.5f;
Color color;
xy = x*x+y*y;
sq = (float)Math.sqrt(xy);
iq = 1f/(xy+1f);
eta = xy-1<=0?-1f:1f;
q1 = half+eta*(half-sq*iq);
q2 = iq/(float)Math.sqrt(6);
q3 = iq/(float)Math.sqrt(2);
r = q1 + 2*x*q2;
g = q1 - x*q2 + y*q3;
b = q1 - x*q2 - y*q3;
color = new Color(r, g, b);
return color;
}